목차

1.Linear
2.SLERP
3.Task Arithmatic
4.TIES Merging
5.Dare
6.Passthrough

모델 병합(Model Merge)은 2개 이상의 대형 언어 모델(LLM)을 추가 학습 없이 단일 모델로 결합하는 혁신적인 기술이다. 이 방법은 개별 모델들의 전문성과 장점을 통합하여 더 광범위한 기능과 향상된 성능을 제공할 수 있으며, 특히 복잡한 작업이나 다양한 도메인에 대한 전문성이 요구될 때 효과적이다. 또한, 별도의 학습 과정이 필요하지 않아 GPT-4와 같은 대규모 모델 학습 시 발생하는 막대한 탄소 배출량과 비용을 획기적으로 줄일 수 있다. 실제로 이 기술은 Open LLM Leaderboard에서 우수한 성과를 보여주었으며, Upstage의 SOLAR 모델과 같은 성공 사례들이 이미 존재한다.

1. Linear

Linear Merge는 여러 모델의 가중치를 가중 평균하여 하나의 통합 모델을 만드는 고전적인 모델 병합 방식이다. 핵심은 각 모델의 동일한 파라미터에 대해, 미리 정해진 가중치를 곱한 후 모두 더하여 가중치 합으로 나누는 것이다. 이 과정은 텐서 단위로 진행되며, 구현이 매우 간단하다는 장점을 가진다.

작동 방식:

1. 가중치 곱셈: 각 모델의 파라미터 값에 해당 모델의 가중치를 곱한다.
2. 합산: 모든 모델의 가중치가 곱해진 파라미터 값을 합산한다.
3. 정규화: 합산된 파라미터 값을 가중치 총합으로 나눈다. 이 과정을 통해 가중 평균을 계산한다.

구현 예시 (mergekit 라이브러리):

res = (weights * tensors).sum(dim=0)  # 가중치 곱셈 후 합산
if self.normalize:
    res = res / weights.sum(dim=0)  # 가중치 총합으로 정규화

위 코드는 mergekit 라이브러리에서 Linear 방법론을 구현한 예시이다. tensors는 병합할 모델의 파라미터 값들을 나타내고, weights는 각 모델에 부여된 가중치를 나타낸다.

Linear 방법론의 장점:

• 구현 용이성: 구현이 매우 간단하고 빠르다.
• 계산 효율성: 복잡한 연산 없이 단순 평균을 사용하므로 계산 비용이 적다.
• 확장성: 다양한 모델과 태스크에 쉽게 적용할 수 있다.

Linear 방법론의 한계점:

• 성능 저하 가능성: 모든 모델이 동일하게 유용하지 않기 때문에, 단순 평균은 오히려 성능 저하나 일반화 능력 손실을 초래할 수 있다.
• 최적 가중치 선정 어려움: 각 모델의 최적 가중치를 자동으로 결정하는 방법이 부족하다.

요약:
Linear 방법론은 모델 병합의 가장 기본적인 방법으로, 구현이 간단하고 계산 효율성이 높다는 장점이 있다. 하지만 성능 저하 가능성, 간섭 문제 미해결 등 몇 가지 심각한 한계점을 가지고 있어, 좀 더 복잡한 병합 방법이 필요할 수 있다.

참고:

• Model Soups: Averaging Weights of Multiple Fine-Tuned Models Improves Accuracy Without Increasing Inference Time

2. SLERP

SLERP (Spherical Linear Interpolation, 구면 선형 보간)는 두 벡터 사이를 부드럽게 보간하는 기법이다. 원래 3D 공간의 회전 처리에 사용되었지만, 모델 병합에서 LERP(선형 보간)의 단점을 보완하여 모델의 성능 저하를 줄이는 효과를 제공한다.

핵심은 벡터의 크기 변화 없이 방향 변화에 집중하여 두 벡터 사이를 보간하는 것이다. 이는 단순히 선형적으로 값을 더하는 것이 아니라, 두 벡터를 구의 표면에 놓고 회전하듯 보간함으로써 구현된다. 이러한 방식으로 벡터의 크기 감소를 방지하고, 벡터 방향의 의미를 최대한 보존힌다.

작동 방식:

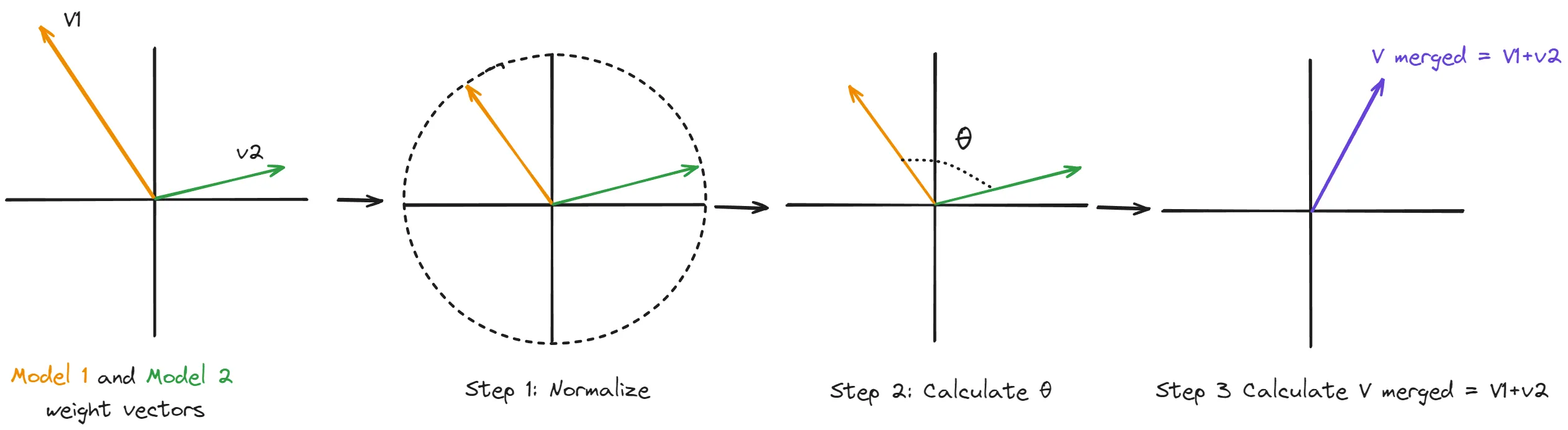
1. 정규화 (Normalize):
   • 두 입력 벡터 (\(v_1\), \(v_2\))를 각각 단위 벡터로 정규화한다. 이는 벡터의 크기 정보를 제거하고 방향 정보만 남겨 벡터가 구 표면에 위치하도록 하는 단계이다.
   • 이 과정을 통해 벡터의 크기가 아닌 방향 정보에 집중할 수 있다.
2. 각도 계산 (Calculate \(\theta\)):
   • 정규화된 두 벡터 사이의 각도 (\(\theta\))를 계산한다. 이 각도는 두 벡터 사이의 상대적인 방향 차이를 나타낸다.
   • 이때 내적(dot product)을 활용하여 코사인 값을 구하고, 아크코사인 함수(arccosine)를 통해 각도를 얻는다.
3. 보간 벡터 계산 (Calculate \(v_{1+2}\)):
   • 보간 계수 t (0에서 1 사이 값, t=0이면 \(v_1\)에 100%, t=1이면 \(v_2\)에 100% 가까움)와 계산된 각도 (\(\theta\))를 사용하여 보간된 벡터 \(v_{1+2}\)를 계산한다.
   • 만약 벡터가 거의 선형에 가까울 경우 (각도가 작을 경우) 효율성을 위해 선형 보간(LERP)을 사용한다. 그렇지 않을 경우, SLERP 공식에 따라 보간 벡터를 계산한다.
   • 보간 벡터는 두 벡터 사이를 부드럽게 회전하면서 보간되어 벡터 크기 감소를 방지하고 방향 정보를 유지한다.

SLERP 구현 코드:

# v1와 v2의 내적 계산
dot = np.dot(v1_copy, v2_copy)
    
# 두 벡터 사이의 초기 각도 계산 (라디안 단위)
theta_0 = np.arccos(dot)
sin_theta_0 = np.sin(theta_0)
 
# 보간 계수 t에 따른 각도 계산
theta_t = theta_0 * t
sin_theta_t = np.sin(theta_t)
 
# slerp 알고리즘 적용
s1 = np.sin(theta_0 - theta_t) / sin_theta_0 # v1에 대한 가중치
s2 = sin_theta_t / sin_theta_0 # v2에 대한 가중치
res = s1 * v1_copy + s2 * v2_copy # 최종 보간된 벡터 계산

SLERP 방법론의 장점:

• 크기 유지: 보간 과정에서 벡터의 크기가 줄어들지 않고 유지된다.
• 부드러운 전환: 두 벡터 사이를 부드럽게 보간하여 파라미터 값의 급격한 변화를 방지한다.
• 방향 정보 보존: 벡터의 방향 정보를 중요하게 여기고, 보간 과정에서 방향 정보를 최대한 보존한다.
• 모델 병합 성능 향상: 모델 파라미터 간의 부드러운 전환을 제공하여 모델 병합 성능을 향상시킨다.

SLERP 방법론의 한계점:

• 2개 모델 제한: 동시에 두 개의 모델만 병합할 수 있다.
• 계산 복잡도: 선형 보간에 비해 계산 복잡도가 높을 수 있다.

SLERP vs Linear:

• Linear: 단순 평균을 사용하여 계산 효율적이지만, 벡터 크기 감소 및 방향 정보 손실 가능성이 있음
• SLERP: 벡터 크기를 유지하고 방향 정보를 보존하며 부드러운 보간을 제공하지만, 계산 복잡도가 더 높고 두 개의 모델만 병합 가능

요약:
SLERP는 모델 병합에서 벡터 크기 감소 문제를 해결하고 방향 정보를 보존하여 더 나은 성능을 제공하는 방법이다. 특히 복잡한 모델 병합 작업에서 파라미터 간의 부드러운 전환을 제공하여 효과적이다.

참고:

• Animating Rotation with Quaternion Curves

3. Task Arithmetic

Task Arithmetic (작업 산술) 방법론은 파인튜닝된 모델의 가중치 변화를 나타내는 ‘Task Vector(작업 벡터)’를 활용하여 모델을 편집하고 새로운 작업을 학습시키는 방법이다. 핵심 아이디어는 각 작업에 대한 모델의 변화를 벡터로 표현하고, 이 벡터들을 더하거나 빼는 방식으로 모델의 행동을 제어하는 것이다.

핵심 개념:

• Task Vector(작업 벡터,\(\tau\)): 파인튜닝된 모델의 가중치에서 사전 학습된 모델의 가중치를 뺀 벡터이다. 각 작업에 대한 모델의 변화 방향과 크기를 나타낸다.
  • \(\tau = \theta_{ft} - \theta_{pre}\) (\(\theta_{ft}\) : 파인튜닝된 모델의 가중치, \(\theta_{pre}\) : 사전 학습된 모델의 가중치)
• Task Arithmetic: 작업 벡터들을 더하거나 빼서 모델의 행동을 변경하는 방식이다. 이를 통해 모델의 성능을 향상시키거나, 특정 작업을 ‘잊게’ 만들거나, 새로운 작업을 학습시킬 수 있다.

작동 방식:

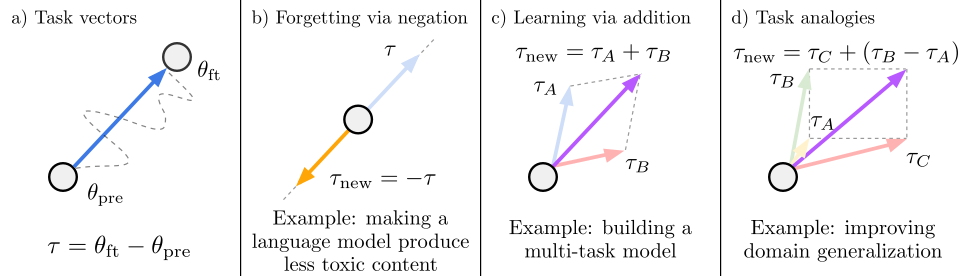
1. 작업 벡터 생성 (Task vectors):
   • 사전 학습된 모델(\(\theta_{pre}\))과 특정 작업에 대해 파인튜닝된 모델(\(\theta_{ft}\))의 가중치 차이를 계산하여 작업 벡터(\(\tau\))를 생성한다.
2. 작업 벡터를 활용한 모델 편집:
   • (b) 망각 (Forgetting via negation):
     특정 작업에 대한 모델의 성능을 감소시키기 위해 해당 작업의 작업 벡터(\(\tau\))에 -1을 곱하여 반대 방향으로 적용한다. (\(\tau_{new} = -\tau\))
     • 예를 들어, 언어 모델이 유해한 콘텐츠를 생성하지 않도록 만드는 경우에 사용된다.
   • (c) 학습 (Learning via addition):
     여러 작업에 대한 성능을 동시에 향상시키기 위해 해당 작업들의 작업 벡터들을 더한다. (\(\tau_{new} = \tau_A + \tau_B\))
     • 예를 들어, 여러 작업을 동시에 수행하는 멀티태스크 모델을 만들 때 사용된다.
   • (d) 작업 유추 (Task analogies):
     기존 작업 벡터들의 관계를 활용하여 새로운 작업을 학습하거나 개선한다. 즉, “A가 B에 대한 것과 같다면, C는 D에 대한 것이다”와 같은 관계를 이용하여 D에 대한 데이터가 없어도 모델의 성능을 개선한다. (\(\tau_{new} = \tau_C + (\tau_B - \tau_A)\))
     • 예를 들어, 도메인 일반화 능력을 향상시키는 데 사용될 수 있다.
3. 병합된 작업 벡터 적용: 병합된 작업 벡터를 기본 모델에 추가하여 원하는 모델 동작을 얻는다.

Task Arithmetic의 장점:

• 효율적인 모델 편집: 모델의 동작을 간단하고 효과적으로 편집할 수 있다.
• 다양한 모델과 작업에 적용 가능: 다양한 모델과 작업에 유연하게 적용할 수 있다.
• 새로운 작업 학습 및 기존 작업 성능 개선: 간단한 산술 연산을 통해 새로운 작업을 학습하거나, 기존 작업의 성능을 향상시킬 수 있다.

Task Arithmetic의 한계점:

• 간섭 문제 고려 미흡: 병합하려는 작업 벡터 간의 잠재적인 간섭을 고려하지 않는다. 이러한 간섭은 모델 성능을 저하시킬 수 있다.
• 최적화 문제: 여러 작업 벡터를 결합하는 최적의 방법 (ex. 가중치 조정)에 대한 연구가 더 필요하다.

요약:
Task Arithmetic은 작업 벡터를 활용하여 모델의 행동을 제어하는 간단하고 효과적인 방법이다. 모델 편집, 멀티태스크 학습, 도메인 일반화 등 다양한 응용 분야에서 활용될 수 있지만, 작업 벡터 간의 간섭 문제를 해결하기 위한 추가적인 연구가 필요하다.

참고:

• Editing Models with Task Arithmetic

4. TIES Merging

TIES Merging (TrIm, Elect Sign & Merge)은 여러 모델을 병합할 때 발생하는 간섭 문제를 해결하여 모델 성능을 향상시키는 방법이다. 특히, 서로 다른 모델이 동일한 파라미터에 대해 다른 방향으로 학습되는 경우 발생하는 부호 간섭 문제를 효과적으로 해결한다. 이러한 간섭은 정보 손실을 초래하여 병합된 모델의 성능을 저해하는 주요 원인으로 작용한다.

핵심 개념:
TIES Merging은 다음과 같은 두 가지 핵심 문제를 해결하여 멀티태스킹 모델 병합을 효과적으로 수행한다.

1. 파라미터 중복성 감소:
   • 각 모델에서 중요하지 않은 파라미터(미세 조정 중 변화가 적은 파라미터)를 제거하여 모델의 중복성을 줄인다.
   • 미세 조정 과정에서 가장 큰 변화를 보인 상위 k%의 파라미터만 유지하고 나머지는 초기값으로 되돌린다.
2. 파라미터 부호 충돌 해결:
   • 서로 다른 모델이 같은 파라미터에 대해 상반된 업데이트 방향(부호)을 가질 때 발생하는 충돌을 해결한다.
   • 각 파라미터의 변화 크기를 고려하여 가장 지배적인 부호 방향을 결정하고, 이 방향에 따라 통합된 부호 벡터를 생성한다.

작동 방식:

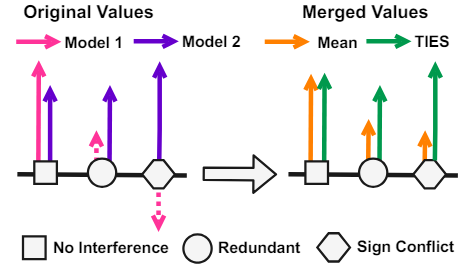
[그림 3]은 다양한 유형의 충돌 및 병합 과정에서 간섭(Interference)이 발생하는 원인을 보여준다. 왼쪽의 Original Values 부분은 여러 모델(Model 1, Model 2)이 학습한 파라미터 값(벡터)들을 나타낸다. 각 파라미터는 네모, 원, 육각형 모양으로 표시되어 있다. 여기서, 네모 모양의 파라미터처럼 비슷한 크기의 벡터가 같은 방향을 가리키는 경우에는 병합 과정에서 정보 손실이 거의 발생하지 않는다. 하지만, 원 모양의 파라미터처럼 한쪽 벡터의 크기가 상대적으로 작거나, 육각형 모양의 파라미터처럼 반대 방향을 가리키는 경우에는 단순 평균을 취할 경우 Merged Values의 Mean 부분과 같이 통합 벡터의 크기가 크게 줄어드는 간섭 현상이 발생하며, 이러한 정보 손실은 최종 모델의 성능 저하로 이어진다. TIES Merging은 이러한 간섭 문제를 해결하기 위해 고안되었다.

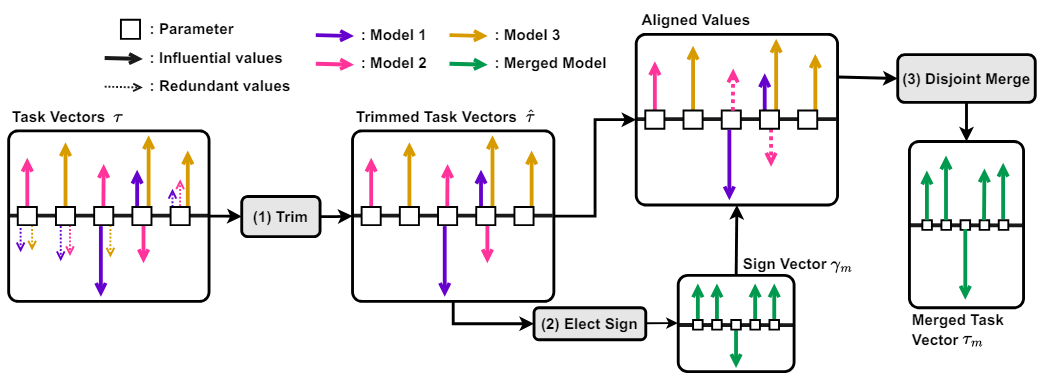
1. Trim (중요 파라미터 선별):
   • 미세 조정 과정에서 가장 큰 변화를 보인 상위 k%의 파라미터만 선택하여 유지하고, 나머지 파라미터는 초기값으로 재설정한다. (Trimmed Task Vectors 부분)
   • 이는 중복 파라미터를 제거하고, 각 모델에서 중요한 정보만 남기는 과정이다. [그림 4]에서 점선으로 표시된 (Redundant values) 파라미터가 제거되는 것을 확인할 수 있다.
2. Elect Sign (통합 부호 결정):
   • 각 파라미터에 대해 모든 모델의 변화 크기(절댓값)를 고려하여 가장 우세한 부호 방향을 결정한다. (Sign Vector 부분)
   • 각 모델의 파라미터 업데이트 방향이 다를 경우, 누적 크기가 가장 큰 방향을 통합 부호로 결정한다. 이를 통해 파라미터 간 부호 충돌을 효과적으로 해결한다. [그림 4]에서 Elect Sign 단계에서 결정된 통합 부호 벡터가 각 파라미터에 적용되는 것을 볼 수 있다.
3. Disjoint Merge (선택적 병합):
   • 이전 단계에서 결정된 통합 부호 벡터와 일치하는 파라미터만 평균을 내어 병합한다. (Merged Task Vector 부분)
   • 이때, Trim 단계에서 제거된 파라미터는 병합 과정에서 제외됩니다.
     • [그림 3]의 Merged Values 부분의 TIES 부분을 보면 간섭이 발생했던 파라미터들도 크기가 유지된 채로 통합된 것을 확인할 수 있다.

TIES Merging의 장점:

• 간섭 문제 해결: 특히 부호 간섭 문제를 효과적으로 해결하여 정보 손실을 최소화한다.
• 성능 향상: 다양한 설정에서 기존 모델 병합 방식보다 우수한 성능을 보여준다.
• 멀티태스킹 학습 효율 증대: 여러 작업별 모델을 하나의 멀티태스킹 모델로 효율적으로 병합할 수 있다.

TIES Merging의 한계점:

• 복잡성 증가: 가중치를 단순히 평균내는 방식에 비해 TIES Merging은 Trim, Elect Sign, Disjoint Merge의 세 단계를 거치므로 복잡성이 증가하고 계산 리소스가 더 많이 필요하다.
• 전문성 필요: TIES Merging을 효과적으로 사용하려면 모델 병합 기술에 대한 전문성이 필요할 수 있다. 특히, Trim 단계에서 파라미터 삭제 임계값 설정, Elect Sign 단계에서 부호 결정 방식 선택이 최종 결과에 큰 영향을 미칠 수 있다.

요약:
TIES Merging은 모델 병합 시 발생하는 간섭 문제를 해결하기 위한 효과적인 접근 방식이다. 파라미터 중복성을 줄이고, 부호 충돌을 해결하며, 선택적인 병합을 통해 성능 향상을 이끌어낸다. 특히 멀티태스킹 학습에 있어 유용한 도구로 활용될 수 있다. 하지만, 구현 복잡성과 전문성이 요구될 수 있다는 단점도 존재한다.

참고:

• TIES-Merging: Resolving Interference When Merging Models

5. DARE

DARE (Drop And REscale)는 모델 병합 시 재학습이나 추가 GPU 자원 없이 효율적으로 모델을 병합할 수 있는 혁신적인 방법이다. DARE의 핵심 아이디어는 파인튜닝된 모델에서 중요하지 않은 파라미터 변화(delta parameter)를 제거하고, 남은 파라미터 변화를 스케일링하여 모델의 성능을 유지하면서 병합하는 것이다.

핵심 개념:

• Delta Parameter (델타 파라미터): 파인튜닝된 모델의 파라미터 값에서 원래 모델(기본 모델)의 파라미터 값을 뺀 차이 값이다. 이 값들은 특정 작업을 수행하도록 모델을 업데이트하는 데 사용된다.
• Drop (삭제): 델타 파라미터 중 일부를 무작위로 0으로 설정(삭제)하는 과정이다. 이를 통해 중요하지 않은 파라미터 변화를 제거한다.
• Rescale (재조정): 삭제되지 않은 델타 파라미터 값을 1/(1-p) 비율로 스케일링하는 과정이다. 여기서 p는 삭제된 파라미터의 비율이다. 이는 삭제로 인해 변경될 수 있는 모델 출력에 대한 기대치를 유지하고 원래 모델의 성능을 보존하는 역할을 한다.

작동 방식:

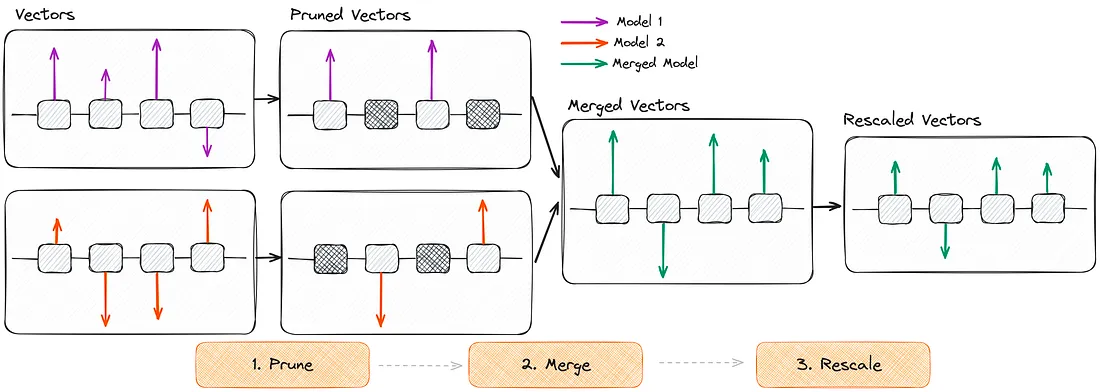
[그림]은 DARE의 작동 단계를 시각적으로 보여준다.

1. Prune (삭제):
   • 각 모델에서 파인튜닝 후 변경된 델타 파라미터 중 일부를 무작위로 0으로 만든다. 이는 모델의 성능에 최소한의 영향을 미치는 파라미터 변화를 제거하는 과정이다. 그림에서 체크무늬로 표시된 부분이 삭제된 파라미터를 나타낸다.
   • 삭제 비율은 p로 지정되며, 일반적으로 90% 이상으로 설정된다. 이렇게 높은 비율로 삭제해도 모델 성능이 유지된다는 점이 DARE의 특징이다.
2. Merge (병합):
   • 삭제된 파라미터를 제외한 나머지 파라미터를 단순히 더하여 병합한다. TIES와 달리 부호 일치를 고려하지 않고 합산하는 방식이 사용된다(dare_linear). 또는 dare_ties 와 같이 TIES에서 사용하는 부호 선택 방식을 활용할 수도 있다.
   • 각 모델의 중요 파라미터 변화를 보존하며 통합한다.
3. Rescale (재조정):
   • 병합된 델타 파라미터에 1/(1-p) 스케일링 팩터를 곱한다. 이를 통해 삭제로 인해 작아질 수 있는 값을 원상 복구시키고 모델 출력에 대한 기대치를 유지한다.
     • 이는 마치 Dropout에서 학습 과정에 적용하는 것과 유사한 방식으로 이해할 수 있다.

DARE 방법론의 장점:

• GPU 자원 및 재학습 불필요: 재학습이나 추가 GPU 자원 없이 모델을 병합할 수 있어 효율적이다.
• 높은 삭제 비율에도 성능 유지: 델타 파라미터 대부분(90% 이상)을 삭제해도 모델 성능이 유지될 수 있다.
• 간섭 문제 회피: 파라미터 삭제를 통해 모델 간 간섭 문제를 명시적으로 해결하려고 시도하지 않고, 삭제 및 재조정 과정을 통해 간섭을 최소화한다.
• 모델 출력 기대치 유지: 삭제 후 남은 파라미터를 재조정하여 모델 출력 기대치를 유지하고, 원래 모델의 성능 특성을 보존한다.

DARE 방법론의 한계점:

• 휴리스틱 의존: 파라미터 삭제가 무작위로 이루어지기 때문에, 휴리스틱에 의존적인 면이 있다.
• 삭제 비율 최적화: 삭제 비율 (p)을 결정하는 최적의 방법에 대한 연구가 더 필요하다.
• 모델 간의 유사성 요구: 동종 모델 간 병합에 주로 사용되며, 서로 다른 특성을 가진 모델을 병합할 때의 효과는 제한적일 수 있다.

DARE vs TIES:

• TIES: 파라미터 중복성을 줄이고 부호 충돌을 해결하여 모델 병합 시 간섭 문제를 해결하려 함
• DARE: 파라미터 변화 중 대부분을 삭제하고 남은 값을 재조정하여 모델 간 간섭 문제를 회피하려 함

요약:
DARE는 모델 병합 시 효율성을 높이고 모델 간 간섭 문제를 피하려는 혁신적인 접근 방식이다. 델타 파라미터의 삭제 및 재조정 과정을 통해 높은 성능을 유지하면서 모델을 효과적으로 병합할 수 있다.

참고:
Language Models are Super Mario: Absorbing Abilities from Homologous Models as a Free Lunch

6. Passthrough

Passthrough (패스스루), 혹은 Frankenmerge (프랑켄머지)라고 불리는 이 방법론은 기존의 모델 병합 방식과는 달리, 서로 다른 모델의 레이어를 연결하여 새로운 모델을 만드는 방법이다. 이러한 방식으로 생성된 모델은 일반적으로 기존 모델보다 더 많은 매개변수를 가지며, 이종의 모델들을 결합하여 새로운 능력을 얻도록 설계되었다. SOLAR-10.7B-v1.0도 논문에서 depth-up scaling이라고 하는 동일한 아이디어를 사용한다 .

핵심 개념:
Passthrough 방법론의 핵심은 다음과 같다:

• 레이어 연결: 서로 다른 모델의 특정 레이어 범위를 선택하여 연결한다.
• 이종 모델 결합: 서로 다른 구조나 특성을 가진 모델들을 결합하여 새로운 모델을 생성한다.
• 매개변수 증가: 일반적으로 기존 모델보다 매개변수 수가 증가한 모델을 생성한다.

작동 방식:

1. 레이어 범위 선택: 병합할 모델들을 선택하고, 각 모델에서 연결할 레이어 범위를 지정한다. 예를 들어, 첫 번째 모델의 레이어 0부터 32까지, 두 번째 모델의 레이어 24부터 32까지를 선택할 수 있다.
2. 레이어 연결: 선택된 레이어들을 순서대로 연결하여 새로운 모델 아키텍처를 구성한다.
3. 모델 생성: 연결된 레이어들을 기반으로 새로운 모델을 생성한다.

구현 예시 (mergekit 설정):

slices:
  - sources:
    - model: OpenPipe/mistral-ft-optimized-1218
      layer_range: [0, 32]
  - sources:
    - model: mlabonne/NeuralHermes-2.5-Mistral-7B
      layer_range: [24, 32]
merge_method: passthrough
dtype: bfloat16

위 설정은 mergekit 라이브러리를 사용하여 Passthrough 방법론을 구현하는 예시이다. 이 설정은 OpenPipe/mistral-ft-optimized-1218 모델의 레이어 0부터 32까지, mlabonne/NeuralHermes-2.5-Mistral-7B 모델의 레이어 24부터 32까지를 연결하여 새로운 모델을 생성한다.

Passthrough 방법론의 장점:

• 모델 용량 증가: 매개변수 수가 증가된 모델을 생성하여 성능 향상 가능성이 있다.
• 모델 특성 결합: 서로 다른 모델의 강점을 결합할 수 있다. 예를 들어, 한 모델의 특정 레이어는 자기 주의 메커니즘을 잘 수행하고, 다른 모델의 레이어는 추론 능력이 뛰어날 수 있다.
• 모델 구조 유연성: 모델 아키텍처에 대한 다양한 실험이 가능한다.
• 새로운 모델 구조 탐색: 기존에 없던 새로운 형태의 모델 구조를 만들 수 있다.

Passthrough 방법론의 한계점:

• 블랙박스 효과: 어떤 레이어 조합이 최적인지 예측하기 어렵고, 모델 동작에 대한 이해가 부족할 수 있다.
• 계산 비용 증가: 매개변수 수가 늘어나 계산 비용이 많이 들 수 있다.
• 성능 저하 가능성: 레이어 조합에 따라 성능이 오히려 저하될 수 있다.
• 최적 조합 찾기 어려움: 최적의 레이어 조합을 찾기 위해서는 많은 시행착오가 필요하다.
• 이종 모델 간 호환성: 서로 다른 구조를 가진 모델들을 결합할 때 호환성 문제가 발생할 수 있다.

Passthrough 방법론 사용 사례:

• 특정 목적 모델 제작: 서로 다른 데이터셋이나 작업으로 학습된 모델을 결합하여 특정 목적에 최적화된 모델을 만들 수 있다.
• 최첨단 모델 결합: 새로운 모델과 기존 모델의 장점을 결합하여 최첨단 모델을 개발하는 데 활용될 수 있다.
• 대규모 모델 생성: 여러 모델을 결합하여 대규모 언어 모델을 생성한다.

요약:
Passthrough 방법론은 서로 다른 모델의 레이어를 연결하여 새로운 모델을 만드는 실험적인 접근 방식이다. 모델 용량을 늘리고 서로 다른 모델의 장점을 결합할 수 있는 잠재력이 있지만, 모델 동작 예측의 어려움, 계산 비용 증가, 성능 저하 가능성 등의 한계점도 가지고 있다.

Conclusion

LLM 병합 기술은 기존 모델들의 강점을 결합하여 더 똑똑하고 유연한 AI를 만드는 동시에, 계산 자원과 에너지 소비를 줄이는 지속 가능한 개발 방식을 제시한다. 레이어 선택의 임의성과 같은 기술적 한계에도 불구하고, SLERP, TIES-Merging, DARE 등 다양한 병합 기법의 발전은 이러한 한계를 극복하는 데 기여하고 있다. 모델 병합 기술은 계속 발전하고 있으며, 진화 기반 방법과 같은 새로운 기술들이 끊임없이 개발되고 있다. 이러한 발전은 고성능 LLM 개발의 기반이 되어, 생성 AI 분야에서 핵심적인 역할을 할 것으로 기대된다.

Reference

• https://github.com/arcee-ai/mergekit
• https://huggingface.co/blog/mlabonne/merge-models
• https://developer.nvidia.com/blog/an-introduction-to-model-merging-for-llms
• https://blog.sionic.ai/llm-merging